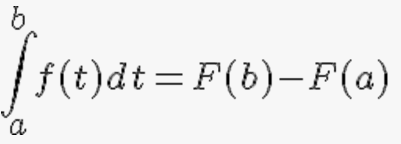formulas de la curvatura

vectores tangente, normal y binormal

https://www.youtube.com/watch?v=_gvD-SUNE3M

Formulas de longitud de arco

la longitud de arco, también llamada rectificación de una curva, es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. Históricamente, ha sido difícil determinar esta longitud en segmentos irregulares; aunque fueron usados varios métodos para curvas específicas, la llegada del cálculo trajo consigo la fórmula general para obtener soluciones cerradas para algunos casos.

Calculo mediante integrales:

Integracion de funciones vectoriales

Integración de Funciones Vectoriales

Una función vectorial es una función definida en términos de la variable tiempo. El rango de esta función es multidimensional dado que la función está constituida por diversos componentes, donde cada uno de los componentes varía con respecto al tiempo en una de las direcciones. Por lo tanto, de manera informal una función vectorial puede denotarse como,

Aquí, cada una de las funciones individuales es una función vectorial de variable real en sí misma. Por lo tanto, el conjunto de funciones (p (t), q (t), r (t)) es una asignación de un intervalo cerrado en Rk, la cual es de rango dimensional k para la función dada. Las dimensiones de entrada y salida de una función vectorial son iguales, las cuales son un vector con alguna forma determinada.

La integración de la función se lleva a cabo mediante la integración de cada uno de los componentes individuales de la función. Por lo tanto la integración de la función vectorial se valora,

Aquí la integración se hace con respecto a ‘t’, la cual es la variable.

Asimismo la integración definida de la función también puede hacerse de la misma manera que una función ordinaria. Para que la integración definida sea llevada a cabo, los componentes completos de la función, y por lo tanto la función misma debe ser real en un intervalo cerrado [a, b]. Si el valor de ‘t’ está incrementandose monótonamente en el intervalo dado o podemos decir que, fi R(t) para i = 1 … k, entonces la integración definida de la función será,

El Teorema Fundamental del Cálculo también se ha modificado para una función valorada vectorial la cual establece que, sean F y f dos funciones diferentes que se trazan con el rango multidimensional Rk para un intervalo cerrado [a, b] también la derivada de F es equivalente a f, entonces

si, f R en [a, b].

Observemos ahora un ejemplo ilustrativo con el fin de tener una mejor comprensión acerca del tema. Calcule la función r(t), dada r’(t) = - y r(0) = + 2 .

Para determinar la función r(t) a partir de las ecuaciones anteriores tenemos que integrar ‘r(t). Pero antes vamos a escribir cada una de las dos funciones en sus formas vectoriales,

r’(t) = <1, −1, 0> r(0) = <0, 1, 2>

Ahora integremos r’(t) como,

  r’(t) dt =  dt -   dt +  dt

r(t) = <t + c1, -t +c2, c1>

Ahora bien, si sustituimos estos valores en la ecuación 2, podemos obtener los valores reales de la constante de integración como,

r(0) = <c1, c2, c3> = <0, 1, 2> c1 = 0 c2 = 1 c3 = 2

Entonces la función r(t) se calcula como <t, -t + 1, 2>.

Por lo general, en el caso que la función vectorial esté en lugar de la constante de integración hacemos uso del vector integración, el cual es un vector arbitrario.

De manera similar, un campo vectorial completo también puede ser integrado lo cual nos ayuda a determinar la cantidad de trabajo realizado por el campo vectorial. Esto se hace tomando la integral de línea del campo vectorial dado.

• Aplicacion de la integracion de funciones vectoriales
• PREVENCION DE TEMBLORES:

UN CAMPO DONDE SE APLICAN LAS FUNCIONES VECTORIALES ES EN LA MEDICION DE LAS ESCALAS DE IMPACTO DEL MOVIMIENTO DE LAS PLACAS TECTONICAS ES DECIR DE LOS TEMBLORES:

SI SE ANALIZARA MAS A FONDO LOS MOVIMIENTOD E LAS PLACAS TECTONICAS Y SE IDENTIFICARAN LO EPICENTROS SERA MAS FACIL Y MAS UTIL EL HECHO DE ANALIZAR ESTOS SISMOS:

Funciones hiperbolicas

Las funciones hiperbólicas son unas funciones cuyas definiciones se basan en la función exponencial, conectando mediante operaciones racionales y son análogas a las funciones trigonométricas estas son:

E

Curvas de la funciones hiperbólicas sinh, cosh ytanh

Curvas de las funciones hiperbólicas csch, sech ycoth

 Aplicaciones de las funciones Hiperbolicas:

El sistema Loran de navegación es una aplicación inmediata de las propiedades de la hipérbola. 

Muchas edificaciones adoptan la hipérbola en sus líneas arquitectónicas: torres en forma de hiperboloide de una hoja, edificios en forma de paraboloide hiperbólico, etc. 

- Techados 

- Estructuras de soporte como columnas y torres Columnas 

-Torres

-Torre de agua