curvas planas y sus ecuaciones paramétricas

Curvas planas y sus ecuaciones paramétricas:
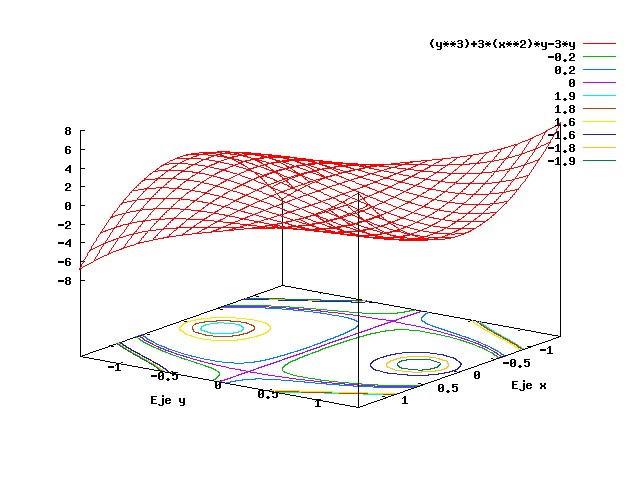
una curva en R2 se puede definir por medio de una ecuación escalar, a la cual por lo general se le da el nombre de función. Esta función consta de dos variables, una de ellas es la variable independiente x mientras que la otra variable, y, se le denomina la Variable Dependiente.

El conjunto de todos los valores que toma la variable independiente x se le llama Dominio de la función, mientras que los valores que se obtienen para la variable dependiente y reciben el nombre de Rango de la Función.

Sin embargo existe otra forma de representar estas funciones ,  consiste en introducir una nueva variable a la que llamaremos Parámetro; esta nueva variable generalmente se representa por las letras r, s ó t. De tal forma que este parámetro pasa a ser ahora la variable independiente y las variables x y y se convierten en las variables dependientes de estas funciones, como se muestra en la siguiente expresión:

x= f(t); y= g(t) en donde t es el parámetro que relaciona a x y y

Ecuaciones paramétricas:
En el análisis Vectorial, este tipo de funciones que generalmente describen curvas en R2, se le llaman Campos Escalares, y la razón es por que en el dominio de la función los valores que toma en  el parámetro son números reales y en el dominio de la función al sustituirse en x y y se obtienen también números reales en el rango.

Ejemplo:

Por ejemplo, podemos estudiar el campo eléctrico en una región del espacio. Entonces en cada punto pondremos un vector cuyo módulo nos indique la intensidad del campo en cada punto. Necesitamos un vector porque el campo eléctrico tiene dirección y sentido.

Ejemplo de campo vectorial

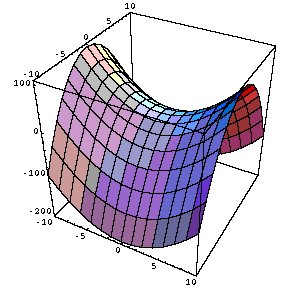
Cuando se habla de un campo escalar lo que nos estamos refiriendo es a una magnitud que viene completamente definida por un número (y sus unidades). Es decir, no tiene ni dirección ni sentido.

Uno podría, idealmente, poner un termómetro en cada punto del suelo de su habitación y anotar la temperatura en cada punto del mismo. Esto nos daría el campo de temperaturas de la superficie del suelo de la habitación.  Un número por cada punto:

Campo de temperaturas del suelo de la habitación. Claramente hay una estufa en el centro . La altura de la figura indica el valor de la temperatura en cada punto del suelo.

En pocas palabras una ecuación paramétrica es aquella en donde encontramos a X y a Y en función de t como en los siguientes ejemplos:

Curvas y superficies de nivel

una curva es: una línea continua de una dimensión, que varía de dirección paulatinamente. Ejemplos sencillos de curvas cerradas son la elipse o la circunferencia, y de curvas abiertas la parábola y la hipérbola. 
en fin, una curva es una linea que hace firuletes en un espacio vectorial. 

superfcie: es un conjunto en 3d, una esfera, un paraboloide hiperbolico,paraboloide, un elipsoide , etc....

LAS CURVAS Y SUPERFICIES NO SON FUNCIONES,SON CONJUNTOS. QUE SE PUEDEN VER COMO "CORTES" DE LOS GRAFICOS QUE DESCRIBEN LAS FUNCIONES. A CADA CORTE DE LA FUNCION SE LO LLAMA NIVEL. 

El conjunto de parejas ordenadas x,y se llama dominio de la función y el conjunto de valores correspondiente a z se llama contra dominio, rango, ámbito. Una función de dos variables se escribe z = “f(x,y) de x, y”.

Las variables x, y se denominan variables independientes y z la variable dependiente.
La gráfica de una función Z es una superficie del espacio tridimensional. El potencial electrostático en un punto P(x,y) del plano debido a una carga puntual unitaria, colocada en el origen está dada por:

Donde C es una constante positiva, las líneas o curvas equipotenciales son círculos alrededor de la carga y se les denomina curvas del nivel 

Las curvas de nivel se usan: en la elaboración de mapas orográficos o planos de configuración.

En los mapas meteorológicos o climáticos, las curvas de nivel se llaman isotérmicos (cuando la temperatura es constante: isotérmico), en un mapa meteorológico que represente la presión atmosférica se les llama isobalos (presión barométrica constante). 

curvas de nivel mas usadas o conocidas: 

circunferencia con centro en (h,j) y radio r: 

(x-h)^2+(y-j)^2=r^2 

elipse con centro en (h,j) y semiejes a y b: 

((x-h)^2)/a^2+((y-j)^2)/b^2=1 

hiperbola: 
(x^2)/a^2-(y^2)/b^2=1 o (y^2)/a^2-(x^2)/b^2=1 

superficies de nivel: 

paraboloide: 
f(x,y)=x^2+y^2 si despejo z me queda 0=x^2+y^2-z 

paraboloide hiperbolico, o silla de montar: 
f(x,y)=x^2-y^2 despejo z entonces me queda 0=x^2+y^2-z 

hiperboloide de una hoja de revolucion: 
1=x^2+y^2-z^2 

hiperboloides de 2 hojas: 
-1=x^2+y^2-z^2 

esfera: 
radio^2=x^2+y^2+z^2 

elipsoide: 

1= (x^2)/a^2 + (y^2)/b^2 +(z^2)/c^2 

notar que en la esfera o en a circunferencia, la formula es la misma que en la elipse o elipsoide pero a=b=c 
y es el radio=a=b=c 

otra cosa cuando restas a x,y,z valores estas corriendo el centro , osea (x-h),(y-j),(z-k) seria centro en (h,j,k) 

para graficar estas cosas online se hace con este programa: 
tan solo tines que escribir la formula y te lo grafica 
http://www.wolframalpha.com/ 

¿quien se ha llevado mi queso?

¿quien se ha llevado mi queso?

es un librito corto pero interesante en forma de parábola,donde nos cuenta una historia dentro de otra sobre dos ratones y dos personitas en busca del queso desaparecido dentro de un laberinto, es una metáfora que nos ayuda a reflexionar sobre los cambios inesperados que tenemos en nuestra vida, sobre el miedo que nos domina, la comodidad y no querer esforzarnos ni adaptarnos a los nuevos cambios y oportunidades, este libro nos ayuda a darnos cuenta que a veces el miedo nos detiene y nos hace mas difíciles las cosas de lo que en realidad son  esta muy recomendado.

link con el libro: ¿quien se ah llevado mi queso?

aqui unas buenas razones para empezar a leer:

Te hace más empática: De acuerdo a un estudio hecho por la Universidad Kenyon, la lectura hace que las personas se vuelvan más amables y empáticas porque, al leer, intercambian su vida con la de alguien más y se tiene una conexión humana, a pesar de que el personaje no exista.

Ayuda a concentrarte: Gracias al Internet y las redes sociales, nuestros cerebros aprenden a estar en todos lados y no concentrarse pero, lo que hace un libro es mantener la mente en su lugar y hacer que se relaje.

Mejora tus conocimientos y vocabulario: ¿No hay nada peor que una chic@ con mala ortografía? Pues este problema podría resolverse fácilmente si la lectura se vuelve un hábito.

Te relaja: La lectura relaja más que un paseo en el parque, una copa de vino, videojuegos, música e incluso tu serie o película favorita.

Mejora tus habilidades de matemáticas: De acuerdo a un estudio británico, las personas que leen por placer, tienen mejores calificaciones en todas sus materias ¡incluyendo matemáticas!

Mantiene a tu cerebro saludable: Para evitar el Alzheimer y darle un empujón a tu mente, es importante que pongas en práctica actividades mentales, como la lectura, para que no se vuelva blanco fácil de este tipo de enfermedades.

planos en R

Cuando se habla de un plano, se está hablando del objeto geométrico que no posee volumen, es decir bidimensional, y que posee un número infinito de rectas y puntos. Sin embargo, cuando el término se utiliza en plural, se está hablando de aquel material que es elaborado como una representación gráfica de superficies en diferentes posiciones. Los planos son especialmente utilizados en ingeniería, arquitectura y diseño ya que sirven para diagramar en una superficie plana o en otras superficies que son regularmente tridimensionales. 

Si en este momento estás leyendo lo que está escrito en esta página, es que miras a la pantalla del ordenador. Te habrás fijado que la pantalla es una superficie lisa, llana, plana,…lo mismo que la tapa de tu pupitre, el cristal de tu ventana, etc.

Todos estos ejemplos representan el plano.

El plano tiene dos dimensiones: largo y ancho:

En el plano podemos dibujar puntos, líneas, etc.

Debes tener presente:
a) Entre dos puntos sólo existe una recta.

b) Por un punto pueden pasar infinitas rectas:

Por el punto P pasan cuantas rectas desees.

A tener en cuenta:
a) Si sobre un plano o superficie plana dibujas una recta, todos sus puntos están contenidos en dicho plano o superficie plana.
b) Un plano puede contener infinitas rectas.

c) Por una recta pueden pasar infinitos planos:

Por la recta r  (en color negro) pueden pasar infinitos planos.

jbdkjhefk