Curvas y superficies de nivel

una curva es: una línea continua de una dimensión, que varía de dirección paulatinamente. Ejemplos sencillos de curvas cerradas son la elipse o la circunferencia, y de curvas abiertas la parábola y la hipérbola. 
en fin, una curva es una linea que hace firuletes en un espacio vectorial. 

superfcie: es un conjunto en 3d, una esfera, un paraboloide hiperbolico,paraboloide, un elipsoide , etc....

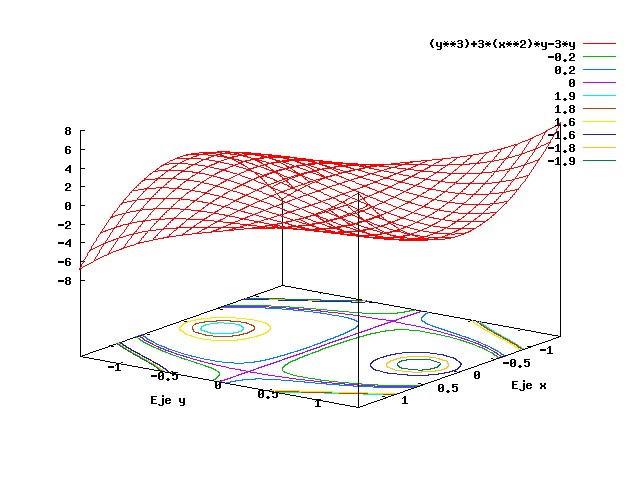
LAS CURVAS Y SUPERFICIES NO SON FUNCIONES,SON CONJUNTOS. QUE SE PUEDEN VER COMO "CORTES" DE LOS GRAFICOS QUE DESCRIBEN LAS FUNCIONES. A CADA CORTE DE LA FUNCION SE LO LLAMA NIVEL. 

El conjunto de parejas ordenadas x,y se llama dominio de la función y el conjunto de valores correspondiente a z se llama contra dominio, rango, ámbito. Una función de dos variables se escribe z = “f(x,y) de x, y”.

Las variables x, y se denominan variables independientes y z la variable dependiente.
La gráfica de una función Z es una superficie del espacio tridimensional. El potencial electrostático en un punto P(x,y) del plano debido a una carga puntual unitaria, colocada en el origen está dada por:

Donde C es una constante positiva, las líneas o curvas equipotenciales son círculos alrededor de la carga y se les denomina curvas del nivel 

Las curvas de nivel se usan: en la elaboración de mapas orográficos o planos de configuración.

En los mapas meteorológicos o climáticos, las curvas de nivel se llaman isotérmicos (cuando la temperatura es constante: isotérmico), en un mapa meteorológico que represente la presión atmosférica se les llama isobalos (presión barométrica constante). 

curvas de nivel mas usadas o conocidas: 

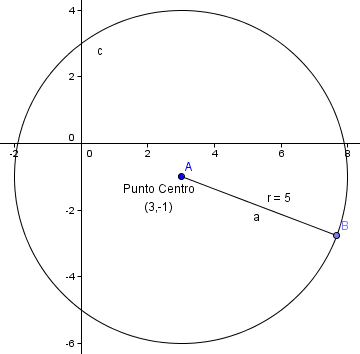
circunferencia con centro en (h,j) y radio r: 

(x-h)^2+(y-j)^2=r^2 

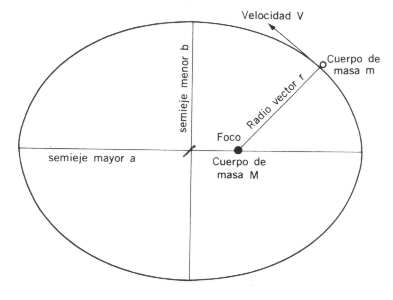
elipse con centro en (h,j) y semiejes a y b: 

((x-h)^2)/a^2+((y-j)^2)/b^2=1 

hiperbola: 
(x^2)/a^2-(y^2)/b^2=1 o (y^2)/a^2-(x^2)/b^2=1 

superficies de nivel: 

paraboloide: 
f(x,y)=x^2+y^2 si despejo z me queda 0=x^2+y^2-z 

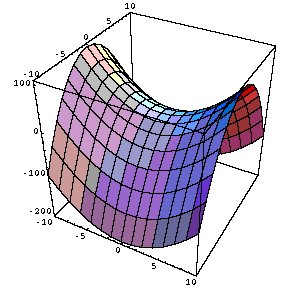
paraboloide hiperbolico, o silla de montar: 
f(x,y)=x^2-y^2 despejo z entonces me queda 0=x^2+y^2-z 

hiperboloide de una hoja de revolucion: 
1=x^2+y^2-z^2 

hiperboloides de 2 hojas: 
-1=x^2+y^2-z^2 

esfera: 
radio^2=x^2+y^2+z^2 

elipsoide: 

1= (x^2)/a^2 + (y^2)/b^2 +(z^2)/c^2 

notar que en la esfera o en a circunferencia, la formula es la misma que en la elipse o elipsoide pero a=b=c 
y es el radio=a=b=c 

otra cosa cuando restas a x,y,z valores estas corriendo el centro , osea (x-h),(y-j),(z-k) seria centro en (h,j,k) 

para graficar estas cosas online se hace con este programa: 
tan solo tines que escribir la formula y te lo grafica 
http://www.wolframalpha.com/